Paprastą harmoninį judesį išrado prancūzų matematikas baronas Jeanas Baptiste'as Josephas Fourieras 1822 m. Edvinas Armstrongas (1890 m. Gruodžio 18 d. - 1954 m. Vasario 1 d.) Savo eksperimentuose stebėjo svyravimus, o Aleksandras Meissneris (1883 m. Rugsėjo 14 d. - 1958 m. osciliatoriai harmonikos terminas yra lotyniškas žodis. Šiame straipsnyje aptariama harmoninio osciliatoriaus apžvalga, apimanti jo apibrėžimą, tipą ir taikymo sritis.

Kas yra harmoninis osciliatorius?

Harmoninis osciliatorius apibrėžiamas kaip judėjimas, kurio jėga yra tiesiogiai proporcinga dalelei iš pusiausvyros taško ir sukuria išvestį sinusine bangos forma. Jėga, sukelianti harmoniką judesio galima matematiškai išreikšti kaip

F = -Kx

Kur,

F = atstatymo jėga

K = pavasario konstanta

X = atstumas nuo pusiausvyros

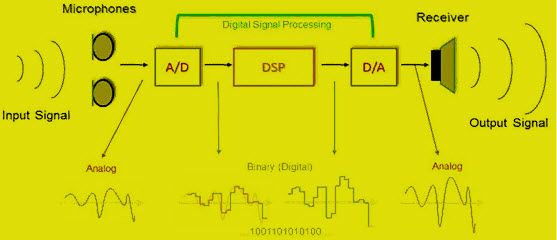
harmonikos-osciliatoriaus blokinė schema

Yra harmoninio judėjimo taškas, kuriame sistema svyruoja, ir jėga, kuri masę vėl ir vėl atneša tame pačiame taške, iš kur ji prasideda, jėga vadinama atstatančia jėga, o taškas - pusiausvyros tašku arba vidutine padėtimi. Šis osciliatorius taip pat žinomas kaip a linijinis harmoninis osciliatorius . Energija teka iš aktyvios komponentai į pasyviuosius komponentus osciliatoriuje.

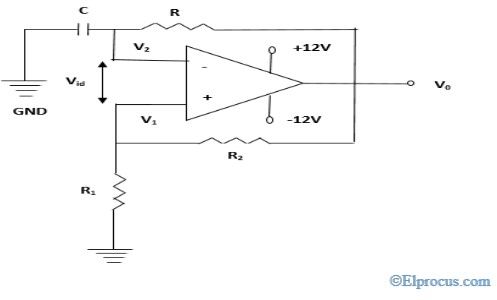
Blokuoti schemą

The harmoninio osciliatoriaus blokinė schema susideda iš stiprintuvas ir grįžtamojo ryšio tinklas. Stiprintuvas naudojamas signalams sustiprinti, o sustiprinti signalai perduodami per grįžtamąjį ryšį ir generuoja išvestį. Kur Vi yra įėjimo įtampa, Vo - išėjimo įtampa, o Vf - grįžtamoji įtampa.

Pavyzdys

Mišios ant pavasario: Spyruoklė suteikia atstatymo jėgą, kuri pagreitina masę, o atkuriamoji jėga išreiškiama kaip

F = ma

Kur „m“ yra masė, o a - pagreitis.

“kaip padaryti integrinius grandynus ”

masė ant pavasario

Pavasaris susideda iš masės (m) ir jėgos (F). Kai jėga traukia masę taške x = 0 ir priklauso tik nuo x - masės padėtis, o spyruoklės konstanta vaizduojama k raide.

Harmoninio osciliatoriaus tipai

Šio osciliatoriaus tipai daugiausia yra šie.

Priverstinis harmoninis osciliatorius

Kai sistemos judėjimui pritaikome išorinę jėgą, sakoma, kad judėjimas yra priverstinis harmoninis osciliatorius.

Slopintas harmoninis osciliatorius

Šis osciliatorius apibrėžiamas taip: kai sistemai veikiame išorinę jėgą, tada osciliatoriaus judėjimas sumažėja ir sakoma, kad jo judėjimas yra slopinamas harmoniniu judesiu. Jie yra trijų tipų slopinamieji harmoniniai osciliatoriai

slopinimo bangos formos

Per slopinta

Kai sistema lėtai juda link pusiausvyros taško, sakoma, kad tai yra pernelyg slopintas harmoninis osciliatorius.

Pagal prislopintą

Kai sistema greitai juda link pusiausvyros taško, sakoma, kad tai yra pernelyg slopintas harmoninis osciliatorius.

Kritinis slopinamas

Kai sistema juda kuo greičiau, nesvyruodama apie pusiausvyros tašką, sakoma, kad tai per daug slopintas harmoninis osciliatorius.

Kvantas

Jį išrado Maxas Bornas, Werneris Heisenbergas ir Wolfgangas Pauli iš „Getingeno universiteto“. Žodis kvantas yra lotyniškas žodis, o kvantinė reikšmė - nedidelis energijos kiekis.

Nulio taškų energija

Nulinio taško energija taip pat žinoma kaip pagrindinės būsenos energija. Jis apibrėžiamas, kai pagrindinės būsenos energija visada yra didesnė už nulį, o šią koncepciją atranda Maxas Planckas Vokietijoje ir formulė, sukurta 1990 m.

Slopintos paprastosios harmoninės osciliatoriaus lygties vidutinė energija

Yra dviejų tipų energijos, tai kinetinė energija ir potenciali energija. Kinetinės energijos ir potencialios energijos suma lygi visai energijai.

E = K + U ………………. Eq (1)

Kur E = bendra energija

K = kinetinė energija

U = potenciali energija

Kur k = k = 1/2 mv^du………… ekv. (2)

U = 1/2 kx^du………… ekv. (3)

svyravimo ciklo - vidutinės vertės

Vidutinės kinetinės ir potencialios energijos vertės per svyravimo ciklą yra lygios

Kur v^du= v^du(Į^du-x^du) ……. ekvivalentas (4)

Eq (4) pakeiskite eq (2) ir eq (3) gausime

k = 1/2 m [masė^du(Į^du-x^du)]

= 1/2 m [Aw cos (wt + ø₀)]^du……. ekvivalentas (5)

U = 1/2 kx^du

= 1/2 k [Nuodėmė (wt + ø₀)]^du……. ekvivalentas (6)

Eq (1) pakaitalai eq (5) ir eq (6) gaus bendrą energijos vertę

E = 1/2 m [masė^du(Į^du-x^du)] + 1/2 kx^du

= 1/2 m pločio^du-1/2 m^duĮ^du+ 1/2 kx^du

= 1/2 m pločio^duĮ^du+1/2 x^du(K-mw^du) ……. ekvivalentas (7)

Kur mw^du= K , pakeiskite šią vertę ekvivalentais (7)

E = 1/2 K A^du- 1/2 Kx^du+ 1/2 x^du= 1/2 K A^du

Bendra energija (E) = 1/2 KA^du

Vidutinės vieno laikotarpio energijos yra išreikštos

Į_vid= U_vid= 1/2 (1/2 K A^du)

Harmoninio osciliatoriaus bangos funkcija

Hamiltono operatorius išreiškiamas kinetinės energijos ir potencialios energijos suma ir išreiškiamas kaip

ђ (Q) = T + V ……………… .ekv. (1)

Kur ђ = Hamitono operatorius

T = kinetinė energija

V = potenciali energija

Norėdami generuoti bangų funkciją, turime žinoti Schrodingerio lygtį, ir lygybė išreiškiama kaip

-đ^du/ 2μ * d^duѱ_υ(Q) / dQ^du+ 1 / 2KQ^duѱ_υ(Q) = E_υѱ_υ(Q) …………. ekvivalentas (2)

Kur Q = įprastos koordinatės ilgis

Μ = efektinė masė

K = jėgos konstanta

Schrodingerio lygties ribinės sąlygos yra:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Eq (2) taip pat galime parašyti kaip

d^duѱ_υ(Q) / dQ^du+ 2μ / đ^du(E_υ-K / 2 * Q^du) ѱ_υ(Q) = 0 ………… ekv. (3)

Parametrai, naudojami sprendžiant lygtį, yra

β = ђ / √μk ……… .. ekv. (4)

d^du/ dQ^du= 1 / β^dud^du/ dx^du………… .. ekv. (5)

Eq (4) ir eq (5) pakeiskite eq (3), tada šio osciliatoriaus diferencialinė lygtis tampa

d^duѱ_υ(Q) / dx^du+ (2μb^duE_υ/ đ^du- x^du) ѱ_υ(x) = 0 ……… .. ekv. (6)

Bendra galios serijų išraiška yra

¬C¬nx2 …………. ekvivalentas (7)

Eksponentinė funkcija išreiškiama

exp (-x^du/ 2) ………… ekv. (8)

eq (7) padauginamas iš eq (8)

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..ekv. (9)

Hermitų polinomai gaunami naudojant žemiau pateiktą lygtį

ђ_υ(x) = (-1)^υ* exp (x^du) d / dx^υ* exp (-x^du) …………… .. ekv. (10)

Normalizuojanti konstanta išreiškiama kaip

N_υ= (1/2^υυ! √Π)^1/2…………… .eq (11)

The paprastas harmoninis osciliatoriaus sprendimas yra išreiškiamas kaip

Ѱ_υ(x) = N_υH_υ(ir) e^{-x2 / 2}……………… ekv. (12)

Kur N_υyra normalizavimo konstanta

H _υyra Hermitas

yra ^{-x2 / du}yra Gauso

(12) lygtis yra harmoninio osciliatoriaus bangos funkcija.

Šioje lentelėje parodyti pirmieji terminai Hermito polinomai, skirti mažiausiai energijos

^υ	0	1	du	3
H_υ(Y)	1	2m	4m^du-2	8m³-12m

Bangos funkcijos paprastas harmoninis osciliatoriaus grafikas keturios mažiausios energijos būsenos parodytos žemiau esančiuose paveiksluose.

bangos-harmonikos- osciliatoriaus funkcijos

harmonikos-osciliatoriaus bangų funkcijos

Šio osciliatoriaus tikimybės tankiai keturioms mažiausiai energijos būsenoms parodyti žemiau esančiuose paveiksluose.

bangos formų tikimybė-tankis

Programos

Šmontuojamas harmoninis osciliatoriusprogramos daugiausia apima šiuos dalykus

Garso ir vaizdo sistemos
Radijas ir kiti ryšio prietaisai
Inverteriai , Aliarmai
„Buzzers“
Dekoratyviniai žibintai

Privalumai

The harmoninio osciliatoriaus pranašumai yra

Pigūs
Aukšto dažnio generavimas
Didelis efektyvumas
Pigūs
Nešiojami
Ekonomiškas

Pavyzdžiai

Šio osciliatoriaus pavyzdyje yra:

Muzikos instrumentai
Paprasta švytuoklė
Masinė spyruoklinė sistema
Sūpynės
Laikrodžio rodyklių judesys
Automobilio, sunkvežimio, autobusų ir kt. Ratų judėjimas

Tai yra vienas judesio tipas, kurį galime stebėti kasdien. Harmonika osciliatorius bangos funkcija naudojant Schrodingerį ir išvestos harmoninio osciliatoriaus lygtys. Čia yra klausimas, kokio tipo judesius atlieka šokinėjimas guma?