Čebyševo filtrų pavadinimas vadinamas „Pafnufy Chebyshev“, nes jo matematinės charakteristikos kildinamos tik iš jo vardo. Čebyševo filtrai yra ne kas kita, o analoginiai arba skaitmeniniai filtrai. Šie filtrai turi kietesnį „roll off“ ir „1“ tipo filtrą (daugiau pralaidumo juostos bangavimo) arba 2 tipo filtrą (stabdymo juostos bangavimą) nei Butterworth filtrai . Šio filtro savybė yra ta, kad jis sumažina paklaidą tarp faktinio ir idealizuoto filtro charakteristikų. Nes, būdingas šiam filtrui pralaidžios juostos bangavimas.
Čebyševo filtras
Chebyševo filtrai naudojami atskiriems vienos juostos dažniams nuo kitos. Jie negali atitikti „Windows-praustuvo“ filtro našumo ir yra tinkami daugeliui programų. Pagrindinė Chebyševo filtro ypatybė yra jų greitis, paprastai didesnis nei „windowed-sinc“. Kadangi šie filtrai atliekami rekursija, o ne konvoliucija. „Chebyshev“ ir „Windowed-Sinc“ filtrų projektavimas priklauso nuo matematinės technikos, vadinamos Z transformacija.

Čebyševo filtras
Čebyševo filtrų tipai
Čebyševo filtrai skirstomi į du tipus, būtent I tipo Chebyševo ir II tipo Chebyševo filtrus.
I tipo Čebyševo filtrai
Šis filtro tipas yra pagrindinis Čebyševo filtro tipas. Amplitudė arba stiprinimo atsakas yra n-osios LPF (žemo dažnio filtro) eilės kampinio dažnio funkcija, lygi visai perdavimo funkcijos Hn (jw) vertei
Gn (w) = | Hn (jω) | = 1√ (1 + ϵ2Tn2 () ω / ωo)
Kur, ε = pulsacijos koeficientas
ωo = ribinis dažnis
Tn = n-tos eilės Čebyševo polinomas
„Pass-band“ rodo lygiavertį pasirodymą. Šioje juostoje filtras keičiasi tarp -1 ir 1, taigi filtro padidėjimas keičiasi tarp max, kai G = 1, ir min, kai G = 1 / √ (1 + ε2). Esant ribiniam dažniui, prieaugio vertė yra 1 / √ (1 + ε2) ir didėjant dažniui, jis lieka nesėkmingas į stabdymo juostą. Filtro veikimas parodytas žemiau. Ribinis dažnis esant -3dB paprastai netaikomas Čebyševo filtrams.

I tipo „Chebyshev“ filtras
Šio filtro tvarka yra panaši į Nr. reaktyviųjų komponentų, reikalingų Čebyševo filtrui naudojant analoginiai prietaisai. Ribliavimas dB yra 20log10 √ (1 + ε2). Kad 3db bangavimo amplitudė atsirastų iš ε = 1. Jei stačiakampį leidžiama stabdymo juostoje, galima rasti dar staigesnį poslinkį, leidžiant komplekso plokštumoje 0 jw ašyje. Nors šis efektas mažiau slopinamas stabdymo juostoje. Poveikis vadinamas „Cauer“ arba elipsiniu filtru.
I tipo Chebyševo filtro lenkai ir nuliai
1 tipo Čebyševo filtro poliai ir nuliai aptariami toliau. Čebyševo filtro polius galima nustatyti pagal filtro stiprinimą.
 -js = cos (θ) & filtro trigonometrikos apibrėžimą galima parašyti taip
-js = cos (θ) & filtro trigonometrikos apibrėžimą galima parašyti taip

Čia θ galima išspręsti

Kur daugybė lankinio kosinuso funkcijos reikšmių paaiškėjo naudojant skaičių indeksą m. Tada Čebyševo polių funkcijos yra
 Naudojant hiperbolinių ir trigonometrinių funkcijų savybes, tai gali būti parašyta tokia forma
Naudojant hiperbolinių ir trigonometrinių funkcijų savybes, tai gali būti parašyta tokia forma

Pirmiau pateikta lygtis sukuria padidėjimo G. polius. Kiekvienam poliui yra sudėtingas konjugatas, o kiekvienai konjugato porai yra dar du neigiami poros neiginiai. TF turėtų būti stabilus, perdavimo funkciją (TF) suteikia

II tipo „Chebyshev“ filtras
II tipas Čebyševo filtras taip pat žinomas kaip atvirkštinis filtras, tokio tipo filtrai yra rečiau paplitę. Nes, jis nesisuka ir jam reikia įvairūs komponentai . Jis neturi bangų pralaidumo juostoje, tačiau turi lygiavertį stabdymo juostoje. II tipo Čebyševo filtro prieaugis yra
 Stabdymo juostoje Chebyševo polinomas keičiasi tarp -1 ir 1, kad padidėjimas „G“ pasikeistų tarp nulio ir
Stabdymo juostoje Chebyševo polinomas keičiasi tarp -1 ir 1, kad padidėjimas „G“ pasikeistų tarp nulio ir

II tipo „Chebyshev“ filtras
 Mažiausias dažnis, kuriuo pasiekiama ši maks, yra ribinis dažnis
Mažiausias dažnis, kuriuo pasiekiama ši maks, yra ribinis dažnis

5 dB stabdymo juostos slopinimo atveju ε vertė yra 0,6801, o 10 dB stabdymo juostos slopinimo atveju ε vertė yra 0,3333. Ribinis dažnis yra f0 = ω0 / 2π0, o 3dB dažnis fH gaunamas kaip
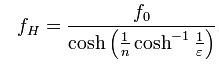 II tipo Čebyševo filtro stulpai ir nuliai
II tipo Čebyševo filtro stulpai ir nuliai
Tarkime, kad ribinis dažnis yra lygus 1, filtro poliai yra stiprinimo vardiklio nuliai
 II tipo filtro stiprinimo poliai yra priešingi I tipo Čebyševo filtro poliams
II tipo filtro stiprinimo poliai yra priešingi I tipo Čebyševo filtro poliams

Čia aukščiau pateiktoje lygtyje m = 1, 2,…, n. II tipo filtro nuliai yra prieaugio skaitiklio nuliai

II tipo Čebyševo filtro nuliai yra priešingi Chebyševo polinomo nuliams.
 Čia m = 1,2,3, ……… n
Čia m = 1,2,3, ……… n
Naudojant kairę pusės plokštumą, TF pateikiama stiprinimo funkcija ir turi panašius nulius, kurie yra viengubi, o ne dvigubi.
Taigi, visa tai yra apie Čebyševo filtrą, Čebyševo filtro tipus, Čebyševo filtro polius ir nulius bei perkėlimo funkcijos skaičiavimą. Tikimės, kad jūs geriau supratote šią koncepciją, be to, turite klausimų apie šią temą ar elektronikos projektai , pateikite savo atsiliepimą komentuodami žemiau esančiame komentarų skyriuje. Štai jums klausimas, kokios yra Čebyševo filtrų programos?
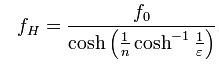 II tipo Čebyševo filtro stulpai ir nuliai
II tipo Čebyševo filtro stulpai ir nuliai